多重解像度解析

多重解像度解析（たじゅうかいぞうどかいせき、英: multiresolution analysis, MRA）とは、2倍毎の解像度のウェーブレットを用いて離散ウェーブレット変換により解析する手法。スケーリング関数で基底展開された信号列を、半分の解像度のスケーリング関数とウェーブレット関数による基底展開の和に分解する。1989年に Stephane G. Mallat が発表した。

本来は異なる物だが、Mathematica や MATLAB をはじめとして、多くのソフトウェアでは多重解像度解析の事を離散ウェーブレット変換と呼んでいる。離散ウェーブレット変換の本来の定義は、離散ウェーブレット変換の項目を参照。

概要

関数 ${\displaystyle f_{j}(x)}$ をスケーリング関数 ${\displaystyle \phi }$ で展開した上で、

${\displaystyle f_{j}(x)=\sum _{k}c_{k}^{(j)}2^{j/2}\phi (2^{j}x-k)=\sum _{k}c_{k}^{(j)}\phi _{j,k}(x)}$

下記のウェーブレット関数 ${\displaystyle \psi }$ への展開を用いて、

${\displaystyle g_{j}(x)=\sum _{k}d_{k}^{(j)}2^{j/2}\psi (2^{j}x-k)=\sum _{k}d_{k}^{(j)}\psi _{j,k}(x)}$

関数 ${\displaystyle f_{j}(x)}$ を異なる解像度（レベル）のウェーブレット関数に展開していく手法を多重解像度解析という。

${\displaystyle f_{j}(x)=g_{j-1}(x) g_{j-2}(x) \cdots g_{j-m}(x) f_{j-m}(x)}$

下記関数集合が基底関数として使われる。

${\displaystyle \{\phi _{j-m,k}(t),\psi _{j-m,k}(t),\cdots ,\psi _{j-1,k}(t)\mid k\in \mathbf {Z} \}}$

スケーリング関数とウェーブレット関数の間にはトゥースケール関係が成立する事が必要である。

トゥースケール関係

以下の関係が成立する場合、トゥースケール関係と呼ぶ。

${\displaystyle \phi (x)=\sum _{k\in \mathbf {Z} }p_{k}\phi (2x-k)}$

${\displaystyle \psi (x)=\sum _{k\in \mathbf {Z} }q_{k}\phi (2x-k)}$

${\displaystyle p_{k},q_{k}}$ の値はウェーブレット関数ごとに異なる。例えばハールウェーブレットの場合は、${\displaystyle p_{0}=p_{1}=q_{0}=1,\ q_{1}=-1}$ 。

トゥースケール関係が成立していると、下記の式が成立する。

${\displaystyle \phi (2x-l)={\frac {1}{2}}\sum _{k\in \mathbf {Z} }(g_{2k-l}\phi (x-k) h_{2k-l}\psi (x-k)),\quad l\in \mathbf {Z} }$

${\displaystyle \{g_{k}\},\{h_{k}\}}$ を分解数列と呼ぶ。例えば、直交ウェーブレットの場合、${\displaystyle g_{k}={\overline {p}}_{-k},\ h_{k}={\overline {q}}_{-k}}$ 。

分解数列が分かると、${\displaystyle f_{j}(x)=g_{j-1}(x) f_{j-1}(x)}$ という変形が可能になり、これを再帰的に繰り返すと多重解像度解析になる。

2次元

2次元の場合は、まず、関数 ${\displaystyle f_{j}(x,y)}$ をスケーリング関数 ${\displaystyle \phi }$ で基底展開する。

${\displaystyle f_{j}(x,y)=\sum _{k_{1}}\sum _{k_{2}}c_{k_{1},k_{2}}^{(j)}2^{j}\phi (2^{j}x-k_{1})\phi (2^{j}y-k_{2})=\sum _{k_{1}}\sum _{k_{2}}c_{k_{1},k_{2}}^{(j)}\phi _{j,k_{1}}(x)\phi _{j,k2}(y)}$

${\displaystyle \phi _{j,k_{1}}(x)\phi _{j,k_{2}}(y)}$ に対して、

${\displaystyle \phi _{j,k_{1}}(x)}$ は ${\displaystyle \phi _{j-1,k_{1}}(x)}$ と ${\displaystyle \psi _{j-1,k_{1}}(x)}$ に分解し、

${\displaystyle \phi _{j,k_{2}}(y)}$ は ${\displaystyle \phi _{j-1,k_{2}}(y)}$ と ${\displaystyle \psi _{j-1,k_{2}}(y)}$ に分解し、

合わせて、

${\displaystyle \{\phi _{j-1,k_{1}}(x)\phi _{j-1,k_{2}}(y),\ \phi _{j-1,k_{1}}(x)\psi _{j-1,k_{2}}(y),\ \psi _{j-1,k_{1}}(x)\phi _{j-1,k_{2}}(y),\ \psi _{j-1,k_{1}}(x)\psi _{j-1,k_{2}}(y)\}}$

の4つに分解する。そして、${\displaystyle \phi _{j-1,k_{1}}(x)\phi _{j-1,k_{2}}(y)}$ を同じように再帰的に分解していく。

結果として、m 回繰り返すと、下記の関数集合が基底関数となる。

${\displaystyle \{\phi _{j-m,k_{1}}(x)\phi _{j-m,k_{2}}(y)\mid k_{1}\in \mathbf {Z} ,k_{2}\in \mathbf {Z} \}\ \cup \ \{\phi _{j_{1},k_{1}}(x)\psi _{j_{1},k_{2}}(y),\ \psi _{j_{1},k_{1}}(x)\phi _{j_{1},k_{2}}(y),\ \psi _{j_{1},k_{1}}(x)\psi _{j_{1},k_{2}}(y)\mid k_{1}\in \mathbf {Z} ,k_{2}\in \mathbf {Z} ,j-1\leq j_{1}\leq j-m\}}$

3次元以上も同じ。

フィルタバンクによる表現

1レベルの変換

信号${\displaystyle x}$の離散ウェーブレット変換は、一組のフィルターを通すことによって計算される。ここではリフティングスキームではなく1989年に発表された手法を説明する。

下記の関係性を満たす ${\displaystyle y_{\mathrm {low} }[k]}$ と ${\displaystyle y_{\mathrm {high} }[k]}$ を ${\displaystyle x[k]}$ から計算するのが離散ウェーブレット変換である。j は入力依存の何らかの整数。${\displaystyle \phi (t)}$ はスケーリング関数、${\displaystyle \psi (t)}$ はウェーブレット関数。

${\displaystyle \sum _{k}x[k]\phi (2^{j}t-k)=\sum _{k}y_{\mathrm {low} }[k]\phi (2^{j-1}t-k) \sum _{k}y_{\mathrm {high} }[k]\psi (2^{j-1}t-k)}$

最初に入力信号列から ${\displaystyle x[k]}$ を計算しないといけないが、ハールウェーブレットや Bior2.2 双直交ウェーブレットの場合は、入力信号の解像度と同じ解像度のスケーリング関数を使えば、${\displaystyle x[k]}$ = 入力信号列になり、特に計算は不要となる。

信号は、インパルス応答が${\displaystyle g}$であるローパスフィルタと、同じく${\displaystyle h}$であるハイパスフィルタを利用して分解される。得られた出力は、ハイパスフィルタから得たものを詳細係数(detail coefficients)、ローパスフィルタから得たものを近似係数(approximation coefficients)とよぶ。これら2つのフィルタは互いに密接な関係があり、直交ミラーフィルタとして知られたものである。

${\displaystyle y_{\mathrm {low} }[n]=\sum \limits _{k=-\infty }^{\infty }{x[k]g[2n-k]}}$

${\displaystyle y_{\mathrm {high} }[n]=\sum \limits _{k=-\infty }^{\infty }{x[k]h[2n-k]}}$

次に、半分にダウンサンプリングを行う。この分解によって、時間解像度は元の信号の半分になり、周波数解像度は2倍となる。これは、ハイゼンベルクの不確定性原理を満たしている。

ダウンサンプリングのオペレータとして${\displaystyle \downarrow }$を使う。

${\displaystyle (y\downarrow k)[n]=y[k\cdot n]}$

以上の式をまとめると以下のようになる。

${\displaystyle y_{\mathrm {low} }=(x*g)\downarrow 2}$

${\displaystyle y_{\mathrm {high} }=(x*h)\downarrow 2}$

しかしながら、${\displaystyle x*g}$の計算の後にダウンサンプリングがあるため、計算に無駄がある。リフティングスキームは、この点を改善している。

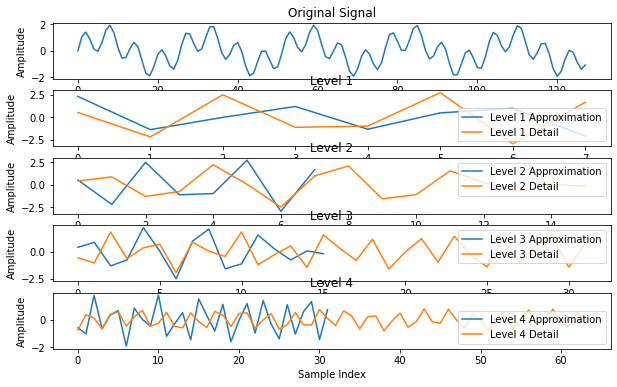
多重解像度解析

この分解は、近似係数を再び分解することによって繰り返され、これを多重解像度解析と呼ぶ。これは、異なる時間周波数の局在性を持った部分空間を枝とする二分木によって表すことが出来る。これはフィルタバンクとして知られているものである。

各々のレベルにおいて、低周波と高周波に分解される。${\displaystyle 2^{n}}$ の長さの入力信号は、ハールウェーブレットの場合は ${\displaystyle n}$ のレベルに分解される。他のウェーブレットの場合も、おおよそ ${\displaystyle n}$ になるが、多少ずれる。

ハールウェーブレットの場合での、32サンプルの信号を例にとる。周波数レンジは0から ${\displaystyle f_{n}}$ であり、3レベルまで分解するとすると、以下の表のようになる。

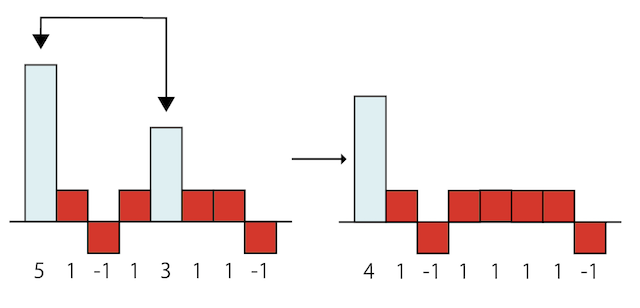
リフティングスキーム

1996年に Wim Sweldens が新しい離散ウェーブレット変換の計算方法であるリフティングスキーム（英: lifting scheme）を発表した。信号を偶数番目の要素と奇数番目の要素に分け、偶数番目の要素で奇数番目の要素を予測し、予測とのズレを高周波成分とし、残差を低周波成分とする手法である。論文の中で、自由に双直交ウェーブレット関数を定義できること、計算が高速化する事を長所に挙げている。ハールウェーブレットと双直交ウェーブレットを扱える。

定義

閉部分空間の系列 ${\displaystyle \left\{V_{j}:j\in \mathbf {Z} \right\}\subset L^{2}(\mathbf {R} )}$ が次の条件1〜5を満たすとき、${\displaystyle \left\{V_{j}\right\}_{j\in \mathbf {Z} }}$ は多重解像度解析を成すという。${\displaystyle A^{c}}$は${\displaystyle A}$ の閉包を表す。

1. ${\displaystyle V_{j}\subset V_{j 1},\ j\in \mathbf {Z} }$
2. ${\displaystyle \cap _{j\in \mathbf {Z} }V_{j}=\{0\},\ (\cup _{j\in \mathbf {Z} }V_{j})^{c}=L^{2}(\mathbf {R} )}$
3. ${\displaystyle f(x)\in V_{j}\Longleftrightarrow f(2x)\in V_{j 1}}$
4. ${\displaystyle f(x)\in V_{0}}$ ならば ${\displaystyle f(x-k)\in V_{0},\ \forall k\in \mathbf {Z} }$
5. ${\displaystyle \phi (x)\in V_{0}}$ が存在して ${\displaystyle \left\{\phi (x-k):k\in \mathbf {Z} \right\}}$ が ${\displaystyle V_{0}}$ においてRiesz基底を成す。すなわち、任意の${\displaystyle f\in V_{0}}$ に対して数列 ${\displaystyle \left\{a_{k}:k\in \mathbf {Z} \right\}\in l^{2}}$ がただ一つ存在して、${\displaystyle f=\sum _{k}a_{k}\phi \left(x-k\right)}$ と表される。さらに定数 ${\displaystyle C_{2}\geq C_{1}>0}$ が存在して、任意の ${\displaystyle \left\{a_{k}:k\in \mathbf {Z} \right\}\in l^{2}}$ に対して不等式 ${\displaystyle C_{1}\|a\|_{2}\leq \|\sum _{j}a_{j}\phi (x-j)\|\leq C_{2}\|a\|_{2}}$ が成立する。

最後の条件はより厳しい条件として、

5'. ${\displaystyle \phi (x)\in V_{0}}$ が存在して、${\displaystyle \left\{\phi (x-k):k\in \mathbf {Z} \right\}}$ が ${\displaystyle V_{0}}$ の正規直交基底となる。

が用いられる事も多い。ここではこの条件5'を用いる。

条件1は空間が入れ子になっていることを意味する。条件2は ${\displaystyle P_{j}}$ を空間 ${\displaystyle V_{j}}$ への直交射影作用素とすると、全ての ${\displaystyle f\in L^{2}(\mathbf {R} )}$ に対して ${\displaystyle \lim _{j\rightarrow \infty }P_{j}f=f}$ であることを意味する。条件3は条件1の全ての空間がスケール変換で得られる事を意味する。条件4は平行移動に対して空間が普遍であることを意味する。

閉部分空間の集まりが条件1〜5'を満たすときには、いつでも正規直交ウェーブレット ${\displaystyle \psi _{j,k}(x)=2^{j/2}\psi (2^{j}x-k)}$ による ${\displaystyle L^{2}(\mathbf {R} )}$ の基底 ${\displaystyle \left\{\psi _{j,k}:j,k\in \mathbf {Z} \right\}}$ が存在し、${\displaystyle P_{j 1}f=P_{j}f \sum _{k\in \mathbf {Z} }\left\langle f,\psi _{j,k}\right\rangle \psi _{j,k}}$ が成立する。

プログラム例

Python（ハールウェーブレット）

ハールウェーブレットの離散ウェーブレット変換は下記のリフティングスキームの数式にて行える。入力を x として、${\displaystyle x_{e}(z)}$ は入力 x の先頭を1番目として偶数番目の要素、つまり、x[1::2]、${\displaystyle x_{o}(z)}$ は奇数番目の要素、つまり、x[0::2]。c が低周波成分（基底関数がスケーリング関数）、d が高周波成分（基底関数がウェーブレット関数）。

${\displaystyle {\begin{pmatrix}c\\d\end{pmatrix}}={\begin{pmatrix}1&1/2\\0&1\end{pmatrix}}{\begin{pmatrix}1&0\\-1&1\end{pmatrix}}{\begin{pmatrix}x_{e}(z)\\x_{o}(z)\end{pmatrix}}}$

ハールウェーブレットの離散ウェーブレット変換のソースコードは下記のようになる。入力は x で NumPy の配列で与える。多重解像度解析をしたい場合は、x = c して長さが1になるまで繰り返す。${\displaystyle \phi _{n,k}(t)={\sqrt {2^{n}}}\phi (2^{n}t-k)}$ の形の基底関数の係数にしたい場合は、c *= sqrt(2) と d /= sqrt(2) をする。

ハールウェーブレットの逆離散ウェーブレット変換のソースコード。

Python（Bior2.2双直交ウェーブレット）

Bior2.2双直交ウェーブレット（2階Bスプライン、線形スプライン）の離散ウェーブレット変換は下記のリフティングスキームの数式にて行える。${\displaystyle z}$ は一つ次の要素、${\displaystyle z^{-1}}$ は一つ前の要素を表す。

${\displaystyle {\begin{pmatrix}c\\d\end{pmatrix}}={\begin{pmatrix}1&(z^{-1} 1)/4\\0&1\end{pmatrix}}{\begin{pmatrix}1&0\\-(1 z)/2&1\end{pmatrix}}{\begin{pmatrix}x_{e}(z)\\x_{o}(z)\end{pmatrix}}}$

Bior2.2の離散ウェーブレット変換のソースコード。配列の境界で足りない分は対称パディングで埋めている。

Bior2.2の逆離散ウェーブレット変換のソースコード。

Java

もっとも単純な例である。ハールウェーブレットによる多重解像度解析をJavaで記述した。

下記コードは上記を逆ウェーブレット変換する。

C言語

C言語による、CDF 9/7 ウェーブレット変換（JPEG-2000で利用）のリフティングを用いた高速な実装は、dwt97.c を参照。

関連項目

• ウェーブレット
• ウェーブレット変換
• 離散ウェーブレット変換

参照